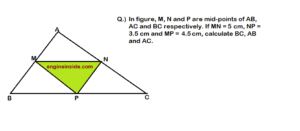
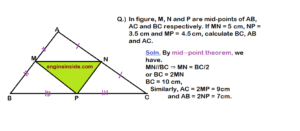

Question 10: In figure, BE ⊥ AC, AD is any line from A to BC intersecting BE in H. P, Q and R are respectively the mid-points of AH, AB and BC. Prove that ∠PQR = 900.

Solution:
BE⊥AC and P, Q and R are respectively mid-point of AH, AB and BC. (Given)
In ΔABC, Q and R are mid-points of AB and BC respectively.
By Mid-point theorem:
QR ∥ AC …..(i)
In ΔABH, Q and P are the mid-points of AB and AH respectively
QP ∥ BH ….(ii)
But, BE⊥AC
From (i) and (ii) we have,
QP⊥QR
⇒∠PQR = 900
Hence Proved.